В
различных жизненных ситуациях нам приходится сталкиваться с явлениями, которые
принято называть случайными. Например:
- время, затрачиваемое студентом на дорогу до института, при
условии, что он едет ежедневно по одному маршруту, будет различным;
- число выбитых очков при стрельбе по мишени одним стрелком
будет различным от тренировки к тренировке.
Неопределенность,
сложность и многопричинность случайных явлений требует специальных методов их
изучения.
Математической теорией,
изучающей закономерности случайных явлений, является ТЕОРИЯ ВЕРОЯТНОСТЕЙ.
В настоящее время аппарат
теории вероятностей используется в областях, связанных с выработкой и принятием
решений в условиях неполной информации, как, например, задачи военного
планирования или экономические задачи.
Для принятия решений нужна информация, на
основе которой решение принимается, и методы, позволяющие эту информацию
собирать, обобщать и анализировать – это задачи математической статистики.
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА разрабатывает методы сбора, обработки и анализа данных.
Основные результаты теории вероятностей -
центральная предельная теорема и
закон больших чисел
являются теоретическими основами математической статистики, таким
образом, обе дисциплины тесно связаны.
Одной из причин быстрого
роста статистических исследований является возрастающая скорость обработки
больших массивов данных. Современные компьютеры при помощи разработанных
пакетов программ статистической обработки данных позволяют в короткое время
проанализировать огромное количество статистической информации и представить ее
для принятия оптимальных решений.
Элементы
комбинаторики
Комбинаторика – это область математики,
определяющая, сколько различных комбинаций, определяемых данными правилами, можно составить из элементов данного
множества (обычно
конечного). Само слово комбинаторика
происходит от латинского слова “combinatio”
(соединение).
В
основе комбинаторики лежат два правила: правило суммы и правило произведения.
Правило
суммы
Если объект 
можно выбрать 
способами, а объект 
- 
способами не такими,
как , то выбор
одного объекта "или , или " можно
осуществить + способами.
Задача 1. Имеются две урны. В первой лежит 10 пронумерованных шаров, в
другой - 8 пронумерованных шаров. Все шары имеют различные номера. Произвольно из какой-нибудь урны вынимается один
шар. Сколькими способами можно вынуть шар с каким-то номером?
Решение. Так как всего имеется 18 шаров с
различными номерами, то вынуть шар с каким-то номером можно 10 + 8 = 18 способами.
Правило
произведения
Если объект можно выбрать способами, а после
каждого такого выбора другой объект можно выбрать,
независимо от выбора объекта , способами, то пары объектов « и » в указанном
порядке можно выбрать ∙ способами.
Задача 2. Имеются две урны. В первой лежит 10 пронумерованных шаров, в
другой - 8 пронумерованных шаров. Все шары имеют различные номера. Из первой
урны вынимается один шар. Из второй урны тоже вынимается один шар. Сколькими
способами можно получить различные пары шаров?
Решение.
Так как каждый шар из первой урны с каждым шаром из второй урны будет
составлять «неповторимую» пару, то всего может быть получено 10 х 8 = 80 различных
пар.
Задача 3. Номера машин в России имеют
следующий код: вначале идет буква, затем трехзначный номер, затем еще две буквы
и затем двузначное число - код региона. Сколько всего можно составить различных
номеров машин, используя такую систему кодификации.
Решение.
В номерах машин используются только буквы, написание которых в русском и в
латинском алфавитах совпадают. Таких букв - 12 (А, В, Е, К, М, Н, О, Р, С, Т, У
и X). Первую букву номера можно выбрать 12 способами. Ненулевых трехзначных чисел
- 999. Каждую из следующих букв также можно выбрать 12 способами. Ненулевых
двузначных чисел - 99. Каждая комбинация букв и чисел есть номер, поэтому всего
номеров может быть: 12∙999∙12∙12∙99 = 170900928.
Рассмотрим
ещё пример: из 10 студентов надо выбрать трех для назначения на дежурство.
Сколькими способами это можно сделать?
Поскольку выбор произволен, то первым
дежурным можно назначить любого, т.е. число способов выбора, очевидно, 
вариантов. Но после
того как выбран первый дежурный, второй выбирается уже из оставшихся 9 человек.
Следовательно, число способов выбора второго дежурного 
вариантов. Ясно, что
третий дежурный выбирается 
способами. Таким
образом, общее число способов выбора равно:
.
Обобщим правило произведения. Если объект можно выбрать из
данного множества способами, объект – способами и так до
k-го выбора, то k объектов вместе могут быть выбраны 
способами.
В
соответствии с этими двумя правилами можно подсчитывать число различных
комбинаций.
Факториал
Понятие
факториала введем для множества 
целых неотрицательных
чисел. Факториалом целого положительного числа n называют произведение 
. Обозначение: «n!».
Читают: «n факториал».
Пример:
.
Принимается: 
и 
.
Факториал можно записать, например,
так: 
или 
.
; 
; 
; 
.
.
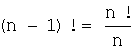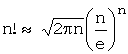Определение. Размещением из n элементов по m называется любое упорядоченное подмножество из m
элементов множества, состоящего из n различных элементов.
Задача
4. Пусть имеется множество,
содержащее четыре буквы: 
. Запишем все возможные размещения из четырех указанных букв
по две. Таких размещений 12:
AB,
AC, AD, BC, BD, CD, BA, CA, DA, CB, DB, DC.
Заметим, что размещения отличаются порядком
входящих в них элементов и их составом. Размещения AB и BA содержат одинаковые
буквы, но порядок их расположения различен. Поэтому эти размещения считаются
разными. Формула для определения числа размещений из n элементов по m имеет
вид: 
(от французского слова “arrangement”, что в
переводе означает "размещение", "приведение в порядок").
Для
приведенного выше примера: 
.
Задача 5. При расследовании хищения установлено, что у преступника
семизначный телефонный номер, в котором ни одна цифра не повторяется, и нет
нулей. Следователь, полагая, что перебор этих номеров потребует одного-двух часов,
доложил о раскрытии преступления. Прав ли он?
Решение: Задача состоит в вычислении числа
комбинаций из девяти различных цифр по 7:
номеров.
Даже если на проверку одного номера тратить
1 минуту, то на все уйдет 3024 часа или 126 суток. Таким образом, следователь –
не прав.
Рассмотрим теперь размещения с повторениями.
Пусть имеется два числа {4; 5}. Из них
можно составить 8 трехзначных чисел:
444, 544, 454, 445, 554, 545, 455, 555, что и иллюстрирует размещение из двух
элементов по три с повторениями.
Определение.
Размещения из n элементов, в каждое из которых входит m элементов, причем один
элемент может повторяться в каждом
размещении любое количество раз,(но не более m) , называются размещениями из n
элементов по m с повторениями.
Формула для расчета: 
Так, для примера, 
.
Задача 6. Пусть стало известно, что в телефонном номере преступника
встречаются только цифры 2, 4, 5 и 7. Насколько уменьшится перебор всех
возможных номеров?
Решение: 
(повт.) = 47 =16384 номера.
Перебрать все эти номера можно примерно за
11 суток.
Рассмотрим теперь отдельно случай, когда m = n. Соответствующие этому
случаю размещения называются перестановками.
Определение.
Перестановкой из n элементов называется любое
упорядоченное множество, в которое входят по одному разу все n различных элементов данного множества.
Пример.
Пусть имеются числа 3, 5, 7. Этому множеству чисел соответствует 6
перестановок: 357, 375, 537, 573, 753, 735.
Число
перестановок n различных элементов обозначается 
(от французского слова “permutation”
– перестановка)
Задача 7. Сколькими способами семь разных учебников
можно поставить на полке в один ряд?
Решение: 
способов.
Рассмотрим теперь случай с повторениями. Если каждый элемент
множества {4; 5} взять по два раза, получим числа: 4455, 5544, 5454, 4545,
4554, 5445.
Определение.
Перестановки из n объектов, в каждую
из которых входят 
одинаковых объектов
одного типа, 
– второго типа и т.д.
до 
– k-го типа, называются перестановками из n
элементов с повторениями.
Число всех таких перестановок с
повторениями:
.
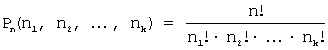Так,
для примера,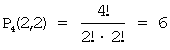 
.
Задача 8. Сколькими способами можно разложить в ряд две зеленые и четыре
красные папки?
Решение: Так как названия папок не
указываются, а критерием является цвет, имеем случай перестановок с
повторениями:
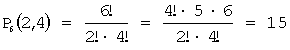способами.
Задача 9. Сколькими способами можно переставить буквы в слове «какао»,
чтобы получились все возможные различные наборы букв?
Решение: В заданном слове – 5 букв, причем
«к» и «а» повторяются по два раза, а «о» встречается один раз: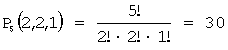 
способов.
Определение. Сочетанием
из n элементов по m называется любое подмножество из m элементов, которые
принадлежат множеству, состоящему из n различных элементов: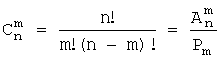 
(от французского слова “combinasion” - сочетание).
Подчеркнем разницу между размещениями и
сочетаниями: в размещениях учитывается порядок входящих в них элементов, а в
сочетаниях – не учитывается.
Задача 10. Необходимо выбрать 4 из 10 имеющихся различных книг. Сколькими
способами можно это сделать?
Решение: 
, то есть число возможных способов выбора равно 210.
Задача 11. В штате мебельного магазина имеется пять грузчиков. Сколькими
способами можно выбрать двух из них для перевозки гарнитура к заказчику?
Решение: Поскольку не имеет значения, какой
грузчик будет первым, а какой – вторым, т.е. необходим выбор двух разных
грузчиков из пяти возможных, то это – задача о сочетаниях из пяти человек по
два. Следовательно, 
способов.
Рассмотрим теперь задачу с повторениями.
Определение. Сочетаниями
с повторениями из n объектов называются множества, содержащие m объектов
(без учета порядка), причем любой объект может входить любое число раз, (но не
более m).
.
Задача 12. Сколькими способами можно выбрать четыре монеты из четырех
пятирублевых и четырех двухрублевых монет?
Решение: Это – задача о числе сочетаний из
двух по четыре с повторениями.Следовательно,
, то есть число таких выборов – пять.
Задача 13. В кондитерской имеется пять разных видов пирожных. Сколькими
способами можно выбрать набор из четырех пирожных?
Решение: Ясно, что можно выбрать как
различные виды пирожных, так и повторяющиеся и даже составить набор из четырех
одинаковых пирожных. Так как порядок пирожных в наборе не имеет значения, то
эта задача относится к классу сочетаний с повторениями. Следовательно,
(повт.)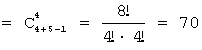 
способами.
