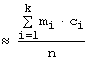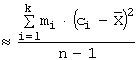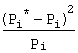ЭЛЕМЕНТЫ
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Математическая статистика - раздел
математики, изучающий математические методы сбора, систематизации, обработки и
интерпретации результатов наблюдений с целью выявления статистических
закономерностей.
Установление
закономерностей, которым подчинены массовые случайные явления, основано на
изучении методами теории вероятностей статистических данных – результатов
наблюдений.
Первая
задача математической статистики – указать способы сбора и группировки
статистических сведений, полученных в результате наблюдений или в результате
специально поставленных экспериментов.
Вторая
задача математической статистики – разработать методы анализа статистических
данных в зависимости от целей исследования. Сюда относятся:
а)оценка неизвестной вероятности события;
оценка неизвестной функции распределения; оценка параметров распределения, вид
которого известен;
б)проверка статистических гипотез о виде
неизвестного распределения или о величине параметров распределения, вид
которого известен.
Итак, задача математической статистики
состоит в создании методов сбора и обработки статистических данных для
получения научных и практических выводов.
Выборочной
совокупностью или просто выборкой
называют совокупность случайно отобранных объектов.
Генеральной
совокупностью называют совокупность
объектов, из которых производится выборка.
Объемом совокупности (выборочной или
генеральной) называют число объектов этой совокупности. Например, если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N = 1000, а объем выборки n = 100.
Статистическое
распределение выборки
Пусть
из генеральной совокупности извлечена выборка объёма n:
![]() , причем x1 наблюдалось m1 раз, x2 – m2 раз и т.д., а
, причем x1 наблюдалось m1 раз, x2 – m2 раз и т.д., а 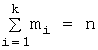 – объем выборки.
– объем выборки. ![]() называют частотами, а
их отношения к объему выборки
называют частотами, а
их отношения к объему выборки ![]() (i=1,2,...k)– относительными
частотами.
(i=1,2,...k)– относительными
частотами.
Статистическим рядом распределения называют перечень
всех значений ![]() из выборки и
соответствующих им частот или относительных частот. Статистическое
распределение можно задать также в виде интервального
статистического ряда, т.е. последовательности интервалов и соответствующих
им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот,
попавших в этот интервал).
из выборки и
соответствующих им частот или относительных частот. Статистическое
распределение можно задать также в виде интервального
статистического ряда, т.е. последовательности интервалов и соответствующих
им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот,
попавших в этот интервал).
Пример. Пусть объем выборки n = 20
и
|
xi |
2 |
6 |
12 |
|
mi |
3 |
10 |
7 |
Найдем
относительные частоты:
![]() ;
; ![]() ;
; ![]() .
.
Тогда
распределение относительных частот:
|
xi |
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Контроль:
![]() .
.
Гистограмма частот

Гистограммой частот называют
ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат
частичные интервалы длиной ![]() , а высоты которых равны отношению
, а высоты которых равны отношению ![]() ,(i=1,2,...k).
Площадь i-го частичного прямоугольника равна
,(i=1,2,...k).
Площадь i-го частичного прямоугольника равна ![]() – относительной
частоте значений выборки, попавших в i-й интервал. Следовательно, вся площадь
равна сумме всех относительных частот, т.е. единице.
– относительной
частоте значений выборки, попавших в i-й интервал. Следовательно, вся площадь
равна сумме всех относительных частот, т.е. единице.
Для
построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а
над ними проводят отрезки, параллельные оси абсцисс на расстоянии ![]() , (i=1,2,...k).
, (i=1,2,...k).
Ступенчатая
кусочно-постоянная линия y = ![]() при
при ![]() , (i=1,2,...k) при стремлении числа интервалов k
, (i=1,2,...k) при стремлении числа интервалов k![]() , а соответственно
, а соответственно ![]()
![]() , превращается в график функции y=f*(x), который является эмпирическим аналогом
дифференциальной функции распределения y=f(x).
, превращается в график функции y=f*(x), который является эмпирическим аналогом
дифференциальной функции распределения y=f(x).
Точечные оценки параметров генеральной совокупности
по выборке
Для
общности обозначим статистическую оценку неизвестного параметра S распределения
(т.е. M(X), D(X) и т.д.) через S* (т.е.![]() и т.д.).
и т.д.).
Точечной статистической оценкой ![]() некоторого параметра
некоторого параметра ![]() генеральной
совокупности (или теоретического распределения случайной величины Х) называется приближенное значение этого
параметра, рассчитанное по данным выборки.
генеральной
совокупности (или теоретического распределения случайной величины Х) называется приближенное значение этого
параметра, рассчитанное по данным выборки.
Иными
словами, точечная статистическая оценка ![]() некоторого параметра
некоторого параметра ![]() генеральной
совокупности (теоретического распределения случайной величины Х) есть некоторая функция выборки (результатов
наблюдений за случайной величиной):
генеральной
совокупности (теоретического распределения случайной величины Х) есть некоторая функция выборки (результатов
наблюдений за случайной величиной): ![]() ,
,
где ![]() - n отобранных элементов генеральной
совокупности, (реализации случайной величины Х в первом, втором, ..., n-ом опытах).
- n отобранных элементов генеральной
совокупности, (реализации случайной величины Х в первом, втором, ..., n-ом опытах).
Во
многих случаях использование числовых характеристик выборки требует ответа на
вопрос: насколько точно выборочные оценки соответствуют статистическим
характеристикам генеральной совокупности, т.е. можно ли утверждать, что
генеральная совокупность описывается числовыми характеристиками конечной
выборки? Сформулируем некоторые критерии, которые следует предъявить к
выборочным оценкам для положительного ответа на поставленный вопрос.
Пусть по выборке объема n найдена оценка S1*.
Повторим опыт – извлечем из генеральной совокупности другую выборку того же
объема и найдем новую оценку S2*.
Повторяя, можно получить числа S1*, S2*, …, Sk*.
Ясно, что выборочные оценки S* можно рассматривать как случайную величину, а
числа S1*, S2*,
…, Sk* как ее возможные значения.
Следовательно, к оценке соответствия характеристик S* и S можно подойти с
вероятностных позиций.
При
получении чисел S1*, S2*, …, Sk*
будут, естественно, случайные отклонения. Но для достаточного числа измерений
можно утверждать, что ![]() ,
,
т.е. математическое ожидание оценки S*
равно оцениваемому параметру S при любом объеме выборки. Такая статистическая
оценка S* называется несмещенной.
Если же равенство не соблюдается, т.е. ![]() , то оценку S* называют смещенной.
, то оценку S* называют смещенной.
Не всегда можно утверждать, что несмещенная
оценка дает хорошее приближение для S. Действительно, возможные значения S*
могут быть сильно рассеяны вокруг своего среднего значения M(S*), т.е.
дисперсия D(S*) может быть значительной. В этом случае, если, к примеру, взять
по одной выборке оценку S1*, то
она может быть сильно удалена от M(S*), а, значит, и от S. Приняв S1*,
мы допустили бы большую ошибку. Но, если потребовать, чтобы дисперсия для S*
была малой, то возможность допустить большую ошибку будет исключена. По этой
причине к S* предъявляется требование эффективности.
Эффективной называют
статистическую оценку S*, которая имеет наименьшую из возможных дисперсию при
заданном объеме выборки n.
И, наконец, при рассмотрении выборок
большого объема, к статистическим оценкам предъявляется требование
состоятельности.
Состоятельной называют
статистическую оценку S*, которая при увеличении объема выборки стремится к
оцениваемому параметру генеральной совокупности, т.е. для любого достаточно
маленького ![]() выполняется следующее
предельное равенство:
выполняется следующее
предельное равенство:
![]() .
.
К примеру, если дисперсия несмещенной
оценки D(S*) при увеличении объема n стремится к нулю, то, очевидно, S* будет и
состоятельной.
Пусть
из генеральной совокупности X извлечена выборка объема n со значениями x1, x2,
…, xn.
В качестве несмещенной, эффективной
состоятельной оценки математического ожидания используют выборочную среднюю: ![]() ;
;
а в качестве оценки дисперсии –
выборочную
дисперсию:
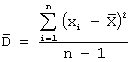 .
.
Для
случая интервального статистического ряда распределения: 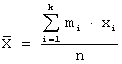
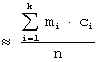 ,
,
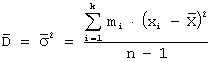
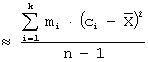 ,
,
где
k - число интервалов, а ![]() - середины
соответствующих интервалов.
- середины
соответствующих интервалов.
Для
вычислений ![]() и
и ![]() по данным эмпирических
наблюдений полезно составлять вспомогательную расчётную таблицу:
по данным эмпирических
наблюдений полезно составлять вспомогательную расчётную таблицу:
|
№ |
Интервалы |
mi |
|
|
|
|
mi(ci |
|
1 |
[х0,х1) |
|
|
|
|
|
|
|
2 |
[х1,х2) |
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
k |
[хк-1,хк) |
|
|
|
|
|
|
|
|
|
частоты |
относительные
частоты |
высоты гистограммы |
середины
интервалов |
|
|
Эмпирическая
функция распределения
Для построения функции распределения необходимо знать значения
вероятностей событий.
Относительная
частота р* появления некоторого события А
в n независимых испытаниях
является несмещенной и эффективной
оценкой вероятности появления этого
события в каждом испытании (![]() ).
).
Для оценки функции распределения случайной
величины Х (генеральной совокупности) по данным
выборки используется понятие эмпирической (статистической) функцией распределения.
Определение. Эмпирической (статистической) функцией распределения называется функция ![]() , определяющая для каждого значения х относительную частоту события р*{Х<x}:
, определяющая для каждого значения х относительную частоту события р*{Х<x}: ![]() .
.
Эмпирическая (статистическая) функция распределения ![]() является
статистическим аналогом функции распределения
является
статистическим аналогом функции распределения ![]() случайной величины Х
(генеральной совокупности), являясь её несмещенной,
состоятельной оценкой.
случайной величины Х
(генеральной совокупности), являясь её несмещенной,
состоятельной оценкой.
Проверка статистической
гипотезы
В процессе статистического анализа часто оказывается
необходимым осуществить проверку некоторых предположений (гипотез)
относительно полученных величин параметров или закона распределения изучаемой
генеральной совокупности.
Статистической гипотезой называется любое предположение о
виде неизвестного закона распределения и значений его параметров. Для
обозначения гипотез используют символ Н.
Выдвинутую (проверяемую) гипотезу обычно называют нулевой (основной). Ее принято обозначать Н0.
По отношению
к высказанной (основной) гипотезе
формулируется также альтернативная (противоположная ей, конкурирующая,)
гипотеза, являющаяся ее логическим отрицанием. Альтернативную (конкурирующую)
гипотезу принято обозначать Н1. Отметим, что для основной гипотезы Н0 может существовать несколько
альтернативных гипотез Н1, Н2, …, Нk . В дальнейшем, однако, ограничимся случаем одной альтернативной
гипотезы Н1.
Правило
(критерий), по которому может быть принята или отвергнута выдвинутая гипотеза,
называется статистическим критерием.
Поскольку проверка статистических гипотез
осуществляется на основании данных выборки
(т. е. ограниченного
ряда наблюдений), принятое решение относительно нулевой гипотезы Н0
может содержать ошибки.
Различают ошибки
двух видов:
1. Отвергнута
верная гипотеза. Такая ошибка называется ошибкой
первого рода, а ее вероятность (обозначаемая символом α) – уровнем
значимости.
Величина
g=(1-α)
называется уровнем доверия(или надёжностью) и определяет вероятность
принять верную гипотезу.
2. Принята
неверная гипотеза. Такая ошибка называется ошибкой второго рода. Вероятность ошибки второго рода
обозначается как ![]() .
.
Величина
(1-![]() ) определяет вероятность принятия гипотезы Н1,
если она верна. Это значение носит название: мощность критерия.
) определяет вероятность принятия гипотезы Н1,
если она верна. Это значение носит название: мощность критерия.
Обычно задается значение вероятности ошибки
1-го рода ![]() (уровень значимости).
При этом часто пользуются ‘стандартными’ значениями для
(уровень значимости).
При этом часто пользуются ‘стандартными’ значениями для ![]() : 0,1; 0,05; 0,025; 0,01; 0,005; 0,001.
: 0,1; 0,05; 0,025; 0,01; 0,005; 0,001.
Статистический критерий определяется правилом или формулой, по
которой оценивается мера близости (расхождения) данных выборки с выдвинутой
гипотезой Н0. Как и всякая функция результатов наблюдения, он
является случайной величиной, а следовательно, может принимать различные
значения, описываемые некоторым законом
распределения. Проверку гипотезы
Н0 о виде закона распределения случайной величины будем
осуществлять с помощью критерия
согласия Пирсона χ2 (хи-квадрат).
Критерий
согласия Пирсона χ2 (хи-квадрат)
Согласно этому критерию сравниваются
относительные частоты ![]() и теоретические вероятности
и теоретические вероятности ![]() . В качестве критерия проверки нулевой гипотезы Н0 находят наблюдаемое значение
случайной величины χ2набл =
. В качестве критерия проверки нулевой гипотезы Н0 находят наблюдаемое значение
случайной величины χ2набл =  .
.
Затем по таблице
критических точек распределения χ2 находят самое большее
допустимое значение χ2кр(α,s), где α - заданный уровень значимости, s - число степеней свободы, s = k – 1 - r, k - число интервалов, r - число параметров предполагаемого распределения.
И сравнивают эти два значения:
если χ2набл <
χ2кр – нет оснований отвергать гипотезу Н0 о виде теоретического закона
распределения генеральной совокупности. Другими словами, эмпирические частоты и
теоретические вероятности различаются незначимо;
если χ2набл >
χ2кр – гипотезу отвергают. Эмпирические частоты и
теоретические вероятности различаются значимо.
Для удобства вычислений χ2набл
полезно составить расчётную таблицу:
|
№ |
Интервалы |
|
Pi |
|
|
1 |
[х0,х1) |
|
|
|
|
2 |
[х1,х2) |
|
|
|
|
|
. . . |
|
|
|
|
к |
[хк-1,хк) |
|
|
|
|
|
|
относительные
частоты |
теоретические
вероятности |
χ2набл
= = |
Заметим, что критерий согласия Пирсона, как и
любой другой критерий, не доказывает справедливость гипотезы, а лишь
устанавливает на принятом уровне значимости α её согласие или несогласие с
данными наблюдений.
Подчеркнём
ещё раз, что уровень значимости α – это вероятность допущенной ошибки,
состоящей в том, что χ2набл ![]() χ2кр,
а гипотеза верна. Т.е. вероятность ошибки
первого рода: отвергнута верная гипотеза.
χ2кр,
а гипотеза верна. Т.е. вероятность ошибки
первого рода: отвергнута верная гипотеза.
Зависимость
χ2кр(α,s)становится
видна из формулы (см. распределение случайной величины χ2):
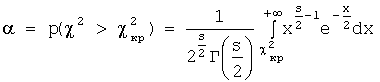 ,
,
по которой
приближённо вычислены значения χ2кр, и составлена в
частности таблица критических точек
распределения χ2 : χ2кр(α,s). Интеграл и гамма-функция зависят только от числа степеней
свободы s.
Заметим
также, что иногда используют другие формы записи критерия, а именно:
χ2набл
= 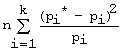
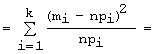
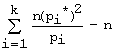 .
.
В
последней формуле учтено, что 
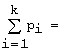 1.
1.
При проверке гипотезы о
нормальном законе распределения генеральной совокупности учитывают, что
число степеней свободы: s = k – 1 – r
= k - 3 (k -
число интервалов), так как число параметров распределения r = 2 ( это математическое ожидание и среднеквадратическое
отклонение).
Теоретические вероятности вычисляют по
формулам:
 , где i=1,2,...k, x0 = -
, где i=1,2,...k, x0 = -![]() xk = +
xk = +![]() ,
,  – функция Лапласа (значения этой функции находят с помощью
таблицы).
– функция Лапласа (значения этой функции находят с помощью
таблицы).
Интервальное
оценивание
Наряду
с точечными оценками (приближенными численными значениями исследуемых
параметров), используются также интервальные
оценки.
Интервальной оценкой параметра q называют числовой интервал (определяемый
его начальной ![]() и конечной
и конечной ![]() точками — концами интервала),
который с заданной вероятностью -
точками — концами интервала),
который с заданной вероятностью - ![]() накрывает
(охватывает) неизвестное значение исследуемого параметра q генеральной совокупности. Интервал, содержащий оцениваемый параметр
генеральной совокупности, называют доверительным
интервалом, а вероятность
накрывает
(охватывает) неизвестное значение исследуемого параметра q генеральной совокупности. Интервал, содержащий оцениваемый параметр
генеральной совокупности, называют доверительным
интервалом, а вероятность ![]() - доверительной вероятностью, уровнем доверия или надежностью оценки.
- доверительной вероятностью, уровнем доверия или надежностью оценки.
Границы
![]() и
и ![]() и величина интервальной
оценки вычисляются по данным выборки и поэтому являются случайными величинами.
и величина интервальной
оценки вычисляются по данным выборки и поэтому являются случайными величинами.
Доверительный
интервал для математического ожидания нормально распределённой случайной
величины при неизвестной дисперсии с заранее заданной надёжностью находят из
формулы:
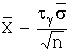
![]()
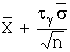 ,
,
![]() находят с помощью
таблицы критических точек распределения Стъюдента:
находят с помощью
таблицы критических точек распределения Стъюдента: ![]() ,
,
n-объём
выборки;
p(
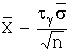
![]()
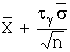 )=
)= ![]() .
.
Коэффициент
регрессии
Статистическое исследование наличия или
отсутствия зависимости между случайными величинами производится с помощью
выборочного коэффициента корреляции. Выделение линейной части этой зависимости
производится с помощью выборочного коэффициента регрессии и выборочного
уравнения (линейной) регрессии.
Если в результате осуществления некоторого
эксперимента наблюдаются две величины ![]() и
и ![]() , то выборочный корреляционный момент
, то выборочный корреляционный момент ![]() величин
величин ![]() и
и ![]() определяется формулой:
определяется формулой:

где ![]() —
— ![]() пар наблюдаемых
значений, полученных в
пар наблюдаемых
значений, полученных в ![]() независимых
повторениях эксперимента,
независимых
повторениях эксперимента, 
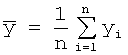 . Выборочный коэффициент
корреляции
. Выборочный коэффициент
корреляции ![]() равен:
равен:
 где
где
![]()

Выборочный коэффициент регрессии ![]() на
на ![]()
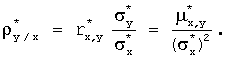
Выборочное уравнение прямой линии регрессии ![]() на
на ![]() имеет вид:
имеет вид:
![]() или
или 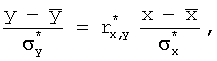
выборочное уравнение прямой
линии регрессии
![]() на
на ![]() :
:
 или
или 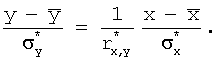
( Эти уравнения выводятся
с помощью метода наименьших квадратов ).