ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

 

   Теория вероятностей – это раздел математики, изучающий закономерности случайных явлений, наблюдаемых при многократном повторении опыта, где под случайным явлением понимаются явления с неопределенным исходом.

   Теория вероятностей занимается изучением закономерностей случайных событий и случайных величин при массовом их появлении.

Примеры случайных явлений:

1. При стрельбе из орудия, установленного под углом к горизонту, фактическая траектория каждого отдельного снаряда отклоняется от теоретической.

2.При различных взвешиваниях на аналитических весах одного и того же тела получаются различные значения.

3.Производится ряд подрывов осколочного снаряда в определенном положении относительно цели. Результаты отдельных подрывов отличаются друг от друга числом осколков, их весом, формой, скоростью, направлением полета осколков и т.д.

   Под опытом (экспериментом, испытанием) понимается воспроизведение определенного (неизменяемого) комплекса условий.

   Результат опыта называется событием (явлением, исходом). События обозначаются заглавными буквами латинского алфавита:A,B,C, …

   Под случайным событием (случайным явлением), понимается такое событие, которое при неоднократном воспроизведении данного опыта иногда происходит, а иногда - нет, причём исход опыта заранее предсказать нельзя.

   Например, при стрельбе по цели (опыт) могут произойти или не произойти попадание или промах.

   Событие называется невозможным (в данном опыте), если при любом повторении опыта оно произойти не может. Такое событие обозначается символом Ø.

   Событие называется достоверным (в данном опыте), если при любом повторении опыта оно обязательно должно произойти. Такое событие

обозначается символом . Так при подбрасывании монеты достоверным является появление орла или решки и невозможным – появление кирпича.

   Несколько событий называются равновозможными, если в рамках данного опыта ни одно из них не является объективно более возможным.

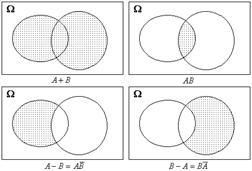
   Суммой двух событий А и В называется событие, обозначаемое как А+В (АВ), и состоящее в наступлении хотя бы одного из этих событий (либо А, либо В, либо А и В вместе).

  Данное определение легко обобщается на случай суммы n>2 событий

 

А₁,А_2,…,А_n…: А₁ + А₂ + … + А_{n …}  =

=  

и определяет событие, состоящее в появлении хотя бы одного из событий(слагаемых) А_i,(i = 1,2,…,n).

   Произведением двух событий А и В называется событие, обозначаемое как А×В (АВ), и состоящее в одновременном наступлении событий А и В. Данное определение также легко обобщается на случай произведения n>2 событий А₁,А_2,…,А_n… и определяет событие, состоящее в одновременном наступлении всех этих событий.

Например. Производится два выстрела по мишени. Пусть событие А – попадание при 1-м выстреле, событие В – попадание при 2-м  выс-

треле. Тогда сумма событий А + В – хотя бы одно попадание при двух выстрелах, произведение А ∙ В – оба попадания.

   Разностью двух событий А и В называется событие, обозначаемое как А-В, и состоящее в одновременном наступлении события А и события, противоположному В (иными словами: наступление события А с одновременным отсутствием события В).

   Опираясь на приведенные выше определения операций, можно показать справедливость следующих выражений:

1) А+А=А;    2) АА=А;

3) А+=;   4) А=А;

5) АØ = Ø;   6) А+ Ø =А,

где   - достоверное событие; Ø - невозможное событие.

Перечислим  также свойства операций сложения и умножения событий:

 

1	A+B = B+A	коммутативность сложения
2	A+(B+С) = (A+B)+С	ассоциативность сложения
3	AB = BA	коммутативность умножения
4	A(B+С) = AB+АС	дистрибутивность умножения

  

 

 

 

 

 

 

 

 

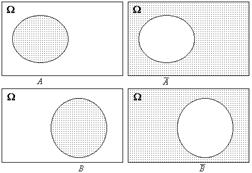
Два события А и В называются несовместными, если их пересечение - пустое множество: А∩В=Ø (или А∙В=0), то есть в результате опыта они не могут произойти одновременно. В противном случае они называются совместными. Так при бросании монеты появление орла и появление решки – несовместные события.

   Некоторое множество событий А₁,А₂,…,А_n образуют полную группу, если в результате опыта происходит хотя бы одно из них. То есть их объединение есть достоверное событие, то есть  (или )

   Если некоторое множество А₁, А_2,…,А_n – полная группа событий и любые два из них несовместны: А_α∩А_β=Ø (α≠β), то в результате опыта происходит одно и только одно из событий данного множества.

   Два события А и В называются противоположными, если появление одного из них исключает появление другого. Иными словами: два события называются противоположными, если они несовместны А∩B=Ø (или А∙В=0) и образуют полную группу  (или А+В=Ω). Событие, противоположное событию  обозначается В =.

Возможные исходы опыта называются элементарными событиями, если они попарно несовместны и образуют полную группу.

  

Вероятность события

 

   Количественной мерой возможности появления события является вероятность. Наиболее широкое распространение имеют два определения вероятности события: классическое и статистическое.

   Статистическое определение вероятности связано с понятием относительной частоты события. Пусть производится серия из  однородных опытов, в которых может появиться или не появиться событие А. Предположим, что событие А появилось в  опытах:  ≤  (по смыслу опытов).

   Относительная частота события вычисляется по формул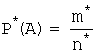е: , где  – число появлений события A в серии из  опытов.

Например: если среди 100 деталей, проверенных ОТК, оказалось 3 бракованных, то относительная частота появления бракованной детали равна 0,03.

Из определения относительной частоты события вытекает, что она всегда удовлетворяет соотношению:  0 ≤  ≤ 1.

   Основной закономерностью многих массовых случайных явлений служит свойство устойчивости частот: говорят, что имеет место устойчивость

частот, если при неограниченном увеличении числа опытов   (то есть при  → ∞) относительная частота события А стремится к некоторому числу:   

Это число Р измеряет степень возможности появления события А в данном опыте.

Число  называется статистической вероятностью события А в данном опыте.

Таким образом, за статистическую вероятность события A принимают то число, относительно которого стабилизируется относительная частота  при увеличении числа опытов.

Например: если много раз подбросить монету, то можно увидеть, что частота выпадения герба (или решки) приближается к 0,5. Из сказанного выше вытекает, что статистическая вероятность удовлетворяет соотношению:  0 ≤ Р ≤ 1.

Свойства вероятности, понимаемой в классической интерпретации, не меняются при переходе к статистической вероятности. Это утверждение основано на следующей теореме Бернулли.

Теорема (сформулирована Я.Бернулли, 1713г.).

   Пусть вероятность появления события А при проведении повторных испытаний постоянна и равна Р(А). При проведении n* независимых испытаний событие А наблюдается m* раз. Тогда, для любого положительного числа ε (ε > 0) имеет место равенство:

,

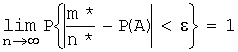иначе говоря относительная частота события А сходится по вероятности к вероятности Р(А).

   Статистическим определением вероятности трудно пользоваться при решении задач, так как вычислить ее в соответствии с определением трудно. Но это понятие важно для практического применения теоретических сведений. В дальнейшем мы будем использовать аксиоматический подход к определению классической вероятности события.  

   Аксиоматика, которой мы будем пользоваться, принадлежит советскому математику А.Н. Колмогорову, и впервые была опубликована в 1933 в книге «Основные понятия теории вероятностей». Мы будем рассматривать аксиоматику Колмогорова в применении к результатам опыта (а не в самом общем абстрактном случае).

 

Классическая вероятность

 

   Рассмотрим некоторый опыт (испытание). Множество результатов этого опыта обозначим: , Предположим, множество:  обладает следующими двумя свойствами:

Свойство 1: Хотя бы один из результатов  достигается в этом опыте обязательно;

Свойство 2: Никакие два различных результата  не могут быть получены в этом опыте одновременно.

   Определение: Если множество результатов опыта ,, обладает свойствами 1 и 2, то это множество Ω называется пространством элементарных событий, а его элементы  элементарными событиями.

Всякое событие А в данном опыте есть подмножество пространства Ω, то есть объединение некоторого множества элементарных событий. Очень удобно представлять пространство элементарных событий Ω в виде некоторой плоской области. Тогда элементарные события представляются как точки этой области, а события – областями внутри Ω.

Само пространство Ω называется достоверным

событием, т.е. таким событием, которое в результате опыта происходит обязательно.

   Пример. Производится 5 выстрелов по цели. Рассмотрим в качестве пространства , 

к = 0,1,2,3,4,5, где ω_k – «к» попаданий при 5 выстрелах. Ясно, что свойства 1 и 2 выполняются, то есть хотя бы одно из ω_k обязательно происходит, а, например, 2 попадания и 4 попадания при пяти выстрелах одновременно произойти не могут. В качестве события А можно, например, рассмотреть:

А={ω₃,ω₄,ω₅}={ω₃ω₄ω₅}–не менее трех попаданий. 

 

Вероятностная схема. Аксиомы вероятности

 

   Определение. Вероятностной схемой в условиях некоторого опыта назовем совокупность следующих трёх объектов:

1.Пространства элементарных событий ;

2.Подмножеств ;

3.Числовой функции, ставящей в соответствие каждому событию А число Р(А), называемое вероятностью и удовлетворяющее следующим аксиомам:

Аксиома1. .

Аксиома2. Р(Ω)=1,  то есть вероятность достоверного события равна 1.

Аксиома3. Если события А₁,А_2,…,А_n попарно несовместны,  то вероятность суммы этих событий равна сумме их вероятностей:

.

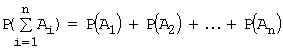Если в единичном опыте обязательно должно произойти одно из попарно несовместных событий , то есть события образуют полную группу, то при этом: .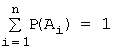

В частности для противоположных событий А и :   

Например, при бросании игральной кости возможно появление одного из чисел: 1,2,3,4,5,6. Вероятность появления каждого числа при единичном бросании , i=1,...6,

 .

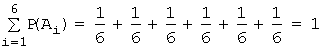   Докажем два свойства вероятности:

   1.Вероятность невозможного события равна нулю: ;

Невозможное событие можно считать противоположным к достоверному: Ø=,  следовательно: Р(Ø)=1–Р()=1–1=0.

   2.Вероятность любого события заключена между нулем и единицей: .

Из аксиомы 1: . Но , следовательно Р(А) ≤ 1.

   Классическое определение вероятности базируется на предположении, что число элементарных исходов конечно, и все они равновозможны (равновероятны):

.

Рассмотрим опыт с пространством элементарных событий ,      

По аксиоме 3: Р(Ω) = , но Р(Ω)=1, поэтому получаем:

 = 1, и так как , то   

Но каждое событие А пространства Ω есть объединение нескольких элементарных событий ,

А, поэтому функция вероятности события Р(А) определяется однозначно: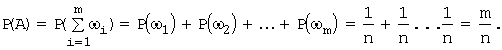

   Определение.  Классической вероятностью

события А называется число равное отношению числа случаев, входящих в событие А (или благоприятствующих событию А), к общему числу случаев в данном опыте:

   Р(А)-вероятность события А; m-число случаев, благоприятствующих событию А; n-общее число случаев.

Случай называется благоприятствующим событию А, если его появление влечет за собой появление события А.

Пример. Найти вероятность того, что в январе наудачу взятого года будет 5 воскресений.

Решение. Так как в январе 31 день, то в любом году в этом месяце бывает 4 или 5 воскресений. Все зависит от того, на какой день приходится 1–е января.

Рассмотрим в качестве пространства элементарных событий  , где – 1–е января – понедельник,  – 1–е января вторник,…, – 1–е января воскресенье. Ясно, что можно считать – равновероятными, всего их n=7 – конечное число. Таким образом, вероятностная схема является классической. Событие А – в январе будет 5 воскресений является объединением 3-х случаев:  По классическому определению вероятности:  

 

 

 

 

 

 

 

 

 

Примеры решения задач на тему «Случайные события. Основные понятия. Классическая вероятность. Элементы комбинаторики»

 

Задача 1. Контролер проверяет партию из 80 телевизоров, среди которых 5 дефектных. Первые три телевизора оказались без дефектов. Какова вероятность, что четвертый окажется с дефектом?

    Решение.

Обозначим:

А – событие, состоящее в том, что четвертый телевизор оказался с дефектом;

    n – общее число возможных исходов для такого события;

    m – число благоприятных исходов для такого события.

Тогда:  n = 80 – 3 = 77; m = 5, отсюда:

Р(А) = .  Ответ:  Р(А) = .

 

Задача 2. Из 20 сотрудников фирмы 8 имеют высшее экономическое образование. Случайным образом отобраны личные дела четырех сотрудников. Какова вероятность того, что:

а) все четверо сотрудников имеют высшее образование?

б) трое из них имеют высшее образование?

    Решение.

    Опыт состоит в выборе четырех личных дел из двадцати. Каждый такой выбор есть сочетание.

а) Обозначим:

А – событие, состоящее в том, что среди отобранных сотрудников все четверо имеют высшее образование;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 4845;    m = C70, отсюда: Р(А) = .

б) Обозначим:

А – событие, состоящее в том, что среди отобранных сотрудников трое имеют высшее образование;   

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 4845;   

m = C672,         отсюда: Р(А) = .

Ответ:  а) Р(А) = 0,0144;     б) Р(А) = 0,1387.

 

     Задача 3. Среди 20 деталей 4 дефектные. Взяты наугад 3 детали. Какова вероятность, что: 

а) все детали дефектные?

б) ровно 2 детали дефектные?

    Решение.

Опыт состоит в выборе трех деталей из двадцати. Каждый такой выбор есть сочетание.

а) Обозначим:

А – событие, состоящее в том, что среди отобранных деталей все дефектные;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n=C1140;   

m=C, отсюда: Р(А) = .

б) Обозначим:

А – событие, состоящее в том, что среди отобранных деталей ровно 2 детали дефектные;  

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 1140;    m = C96,         отсюда:

            Р(А) = .

Ответ: а) Р(А) = 0,0035;       б) Р(А) = 0,0842

 

Задача 4. На торговой выставке представлены 12 приборов данной фирмы. Из них 7 высшего класса точности. Для демонстрации произвольно берут 4 прибора. Какова вероятность, что:

а) все они окажутся высшего класса?

б) ровно три из них высшего класса?

    Решение.

Опыт состоит в выборе четырех приборов из двенадцати. Каждый такой выбор есть сочетание

а) Обозначим:

А – событие, состоящее в том, что среди отобранных приборов все окажутся высшего класса;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 495;   

m=C, отсюда:Р(А) = .

б) Обозначим:

А – событие, состоящее в том, что среди отобранных приборов ровно 3 окажутся высшего класса;   

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 495;   

m = C175,         отсюда:

            Р(А) = .

Ответ: а) Р(А) = 0,0707;      б) Р(А) = 0,3535.

 

Задача 5. Руководство компании, проводя кадровую политику, заранее намечает кандидатуры на выдвижение. Имеются 9 кандидатов на должности начальников отделов, из них 4 женаты. Появились 3 вакантные должности начальников отделов. Если они будут выбираться из девяти кандидатов случайным образом, какова вероятность того, что

а) все 3 выбранных начальника отделов окажутся женаты?

б) ровно 2 выбранных начальника отделов окажутся женаты?

    Решение.

Опыт состоит в выборе трех кандидатов из девяти. Каждый такой выбор есть сочетание

а) Обозначим:

А – событие, состоящее в том, что среди отобранных кандидатов все окажутся женаты;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C84 ;   

m=C, отсюда:Р(А) = .

б) Обозначим:

А – событие, состоящее в том, что среди отобранных кандидатов ровно 2 окажутся женаты;

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда: n = C84 ;   

m = C30,         отсюда:

            Р(А) = .

Ответ: а) Р(А) = 0,0476;      б) Р(А) = 0,3571.

 

Задача 6. Известно, что Герман в "Пиковой даме" должен из колоды в 52 карты вытянуть подряд тройку, семерку, туз. Каковы его шансы на успех, если:

а) эти карты должны быть одной масти?

б) эти карты могут быть любой масти?

    Решение.

Опыт состоит в выборе трех карт из пятидесяти двух в определенном порядке. Каждое такое действие есть размещение.

а) Обозначим:

А – событие, состоящее в том, что вытянуты подряд тройка, семерка, туз одной масти;

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события;

m₁ – число выборов первой карты (тройки);

m₂ - число выборов второй карты (семерки);

m₃ - число выборов третьей карты (туза).

Тогда:n=; m=m₁∙m₂∙m₃=4∙1∙1=4; отсюда: Р(А)= .

б) Обозначим:

А – событие, состоящее в том, что вытянуты подряд тройка, семерка, туз любой масти;

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события;

m₁ – число выборов первой карты (тройки);

m₂ - число выборов второй карты (семерки);

m₃ - число выборов третьей карты (туза).

Тогда:n=; m= m₁∙m₂∙m₃=4∙4∙4=64; отсюда: Р(А) = .

Ответ:   а) Р(А) = 0,000134; б) Р(А) = 0,00215.

 

Задача 7. Программа курса "Математическая статистика" содержит 30 теоретических вопросов. Студент выучил к экзамену только 26 вопросов. Экзаменационный билет содержит 2 теоретических вопроса. Студент взял билет. Какова вероятность того, что

а)  студент знает оба вопроса билета?

б)  студент знает ровно один вопрос билета?

в) студент не знает ни одного вопроса билета?

    Решение.

Опыт состоит в выборе двух вопросов из тридцати. Каждый такой выбор есть сочетание.

а) Обозначим:

А – событие, состоящее в том, что студент знает оба вопроса билета;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 435;   

m = C, отсюда:

            Р(А) = .

б) Обозначим:

А – событие, состоящее в том, что студент знает ровно один вопрос билета;

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда:      n = C 435;  

m=C104,         отсюда:

            Р(А) = .

в) Обозначим:

А – событие, состоящее в том, что студент не знает ни одного вопроса билета;  

n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда: n = C 435;   

m = 6,   отсюда:Р(А)=.

 

Ответ: а) Р(А) = 0,7471;      б) Р(А) = 0,2391;     в) Р(А) = 0,0138.

 

Задача 8. Управление милиции выделило три премии для сотрудников оперативных подразделений. В фуражку начальника положили 8 карточек с фамилиями восьми сотрудников. Какова вероятность того, что первую премию получит следователь Зубов, вторую – оперативный сотрудник Прокопенко, третью – эксперт-криминалист Васильева?

 

    Решение.

Опыт состоит в выборе трех сотрудников из восьми и распределении их по номерам премий. Каждое такое действие есть размещение.

Обозначим:

А – событие, состоящее в том, что первую премию получит следователь Зубов, вторую – оперативный сотрудник Прокопенко, третью – эксперт-криминалист Васильева;

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Тогда: n = ;    m = 1,

т.к. нас интересует только одно размещение:

Р(А) = . Ответ: Р(А) = 0,00298.

 

Задача 9. Библиотечка состоит из десяти различных книг: пять книг по 400 рублей каждая, три книги - по 100 рублей, две книги – по 300 рублей. Найти вероятность того, что взятые наудачу две книги стоят 500 рублей.

    Решение.

    Опыт состоит в выборе двух книг из десяти. Выбор любых двух книг из десяти есть сочетание.

Обозначим:

    А – событие, состоящее в том, что взятые наудачу две книги стоят 500 рублей;  

    n – общее число возможных исходов для такого опыта;

    m – число благоприятных исходов для такого события.

Событие А реализуется только в том случае, если будет выбрана одна книга стоимостью 400 рублей и одна книга стоимостью 100 рублей.

Тогда:      n = C;   

m=C,         отсюда: Р(А) = . Ответ: Р(А) = .

     Задача 10. Брошены два игральных кубика. Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение – четырем.

     Решение: Каждый кубик при бросании дает одно из чисел 1,2,3,4,5,6. Так как оба кубика бросаются независимо, то по теореме умножения общее число исходов: 6·6 = 36.

Ясно, что удовлетворить условию задачи возможно только двумя сочетаниями очков: 1, 4 или 4, 1. То есть только два исхода благоприятствуют условию задачи. Следовательно, по определению вероятности:  .

 

     Задача 11. В коробке имеется 15 шаров, из которых 10 – окрашены, а 5 – прозрачные. Извлекаем, не глядя, три шара. Какова вероятность того, что все они будут окрашены?

     Решение: Общее число исходов при извлечении шаров: .

Благоприятных исходов того, что все шары окрашены: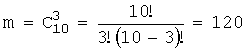. Следовательно, .

 

     Задача 12. В библиотеке на стеллаже расставлено 15 учебников по математике, причем только 5 из них пригодны для студентов инженерного факультета. Студент наудачу выбирает 3 учебника. Какова вероятность того, что хотя бы один из учебников – тот, что нужен?

     Решение: Всего три учебника из 15 можно выбрать:

 способами.

Ненужные учебники при этом (из 10 шт.) могут быть выбраны:

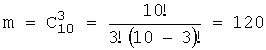 способами.

Следовательно, вероятность того, что все учебники непригодны: .

Поскольку события А – «хотя бы один учебник пригоден» и  – «все три учебника непригодны» противоположны и составляют полную группу, то , следовательно, .