Формула и схема
Бернулли
Пусть
многократно реализуются повторные испытания при неизменных условиях их
проведения. В ходе испытания фиксируется появление некоторого случайного
события А, вероятность
появления которого – Р(А) не
зависит от результатов предыдущих испытаний и остается неизменной ( Р(А)=const ) при
повторении опыта. Такие испытания
называются независимыми, а
схема проведения испытаний носит название схемы Бернулли.
Вероятность 
того, что событие А наступит ровно m раз в n независимых испытаниях, удовлетворяющих условиям схемы
Бернулли равна:
,
где
:p=P(A)–вероятность
наступления события А; и q=1-p.
Пример 1. Вероятность выигрыша по лотерейному билету
равна 0,05. Какова вероятность того, что
среди купленных 10 билетов окажутся 2 выигрышных.
Решение. Данная задача описывается схемой Бернулли:
проводится 10 испытаний, в ходе которых проверяется наличие выигрыша. Применяя
формулу Бернулли, находим вероятность появления выигрыша в двух из десяти
испытаний:
.
Пример 2. При проведении маркетинговых исследований
выявлено, что 20% опрошенных предпочитают использовать продукцию данной фирмы.
Найти вероятности возможного числа пользователей продукцией фирмы в произвольно
выбранной группе из пяти человек.
Решение. Согласно условию
задачи вероятность того, что человек использует продукцию данной фирмы равна
0,2 (т.е: 
и 
). Искомые вероятности находим по формуле Бернулли (где: n=5;
и m=1,…,5)
и помещаем их в таблицу.
|
№ п.п. |
Число
пользователей продукцией фирмы в
группе из пяти человек |
Вероятность
рассматриваемого события ( |
|
1 |
Пользователей
нет |
|
|
2 |
Один
пользователь |
|
|
3 |
Два
пользователя |
|
|
3 |
Три пользователя |
|
|
4 |
Четыре
пользователя |
|
|
5 |
Все
используют продукцию данной
фирмы |
|
Асимптотические
приближения формулы Бернулли
Формула Бернулли дает точное значение
вероятности того, что событие А
наступит ровно m раз в n независимых испытаниях,
определяемых схемой Бернулли. Однако, практическое применение этой формулы
часто оказывается затруднительным, если числа m и n достаточно
велики, а вероятность р – мала.
Существуют некоторые асимптотические приближения формулы Бернулли.
Формула Пуассона
Теорема. Если
вероятность p
наступления некоторого события А
в каждом испытании, определяемом схемой Бернулли, стремится к нулю (
) при неограниченном увеличении числа испытаний n (
), а произведение np стремится к некоторой константе 
(
), то вероятность того, что событие А наступит
ровно m раз в n испытаниях удовлетворяет
предельному равенству: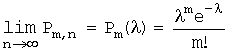 
.
С практической точки зрения, условия и
выводы данной теоремы означают, что при выполнении следующих трех условий:
а)вероятность p наступления некоторого события А в каждом испытании, определяемом схемой Бернулли, достаточно
мала;
б)число
испытаний n – велико;
в)произведение np не превышает десяти (
),
то с достаточно высокой степенью точности
формула Бернулли может быть аппроксимирована
следующей формулой (Пуассона):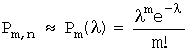 
, где: 
.
Локальная формула
Муавра-Лапласа
Теорема. (локальная теорема Муавра-Лапласа). Если
вероятность p
наступления события А в каждом
испытании, определяемом схемой Бернулли, постоянна и отлична от 0 и 1 (
и 
), а число испытаний n достаточно велико, то
вероятность того, что событие А наступит ровно m раз в n испытаниях приближенно равна:
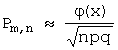, где: φ(x) - функция Гаусса, определяемая
выражением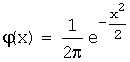 
, аргумент х
которой вычисляется по формуле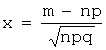 
.
Точность данного приближения увеличивается
с ростом n(n>>1), и на практике оно может быть
использовано при значении n, удовлетворяющих условию: 
.
Значения
функции Гаусса табулированы, что упрощает проведение расчётов.
Полезно
иметь в виду следующие свойства функции Гаусса:
1.Для положительных
значений х, функция Гаусса φ(x) является монотонно убывающей, стремящейся к нулю
функцией: 
.
2.Для
области отрицательных значений аргумента, свойства функции Гаусса φ(x) определяются ее четностью: φ(-x)= φ(x).
Интегральная
теорема Муавра-Лапласа
Часто
на практике требуется найти вероятность того, что число наступлений события А находится в некотором диапазоне.
Например, требуется найти вероятность того, что событие А произойдет от десяти пятнадцати раз. Ответ на этот вопрос
помогает найти следующая теорема.
Теорема. (интегральная теорема
Муавра-Лапласа). Если вероятность p наступления некоторого события А в каждом испытании, определяемом
схемой Бернулли, постоянна и отлична от 0 и 1 ( и ), то вероятность того, что число m наступлений события А в n испытаниях заключено в интервале [a, b] - 
, при достаточно большом n, приближенно равна: 
,
где: 
- функция, именуемая интеграл
вероятности Лапласа, определяется
выражением:
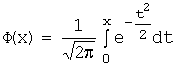,а значения 
и 
вычисляются по
формулам: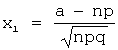 
, 
.
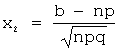Приведенная
выше формула вычисления вероятности носит название интегральной формулы Муавра-Лапласа.
Ее точность возрастает с ростом n(n>>1), а ее применение на практике обычно выражается условием,
аналогичным для локальной формулы: .
Значения
функции (интеграл
вероятности Лапласа) табулированы. При проведении соответствующих
расчетов полезно иметь в виду свойства функции , о которых подробно рассказано
в разделе “Нормальный закон распределения”.
Примеры
решения задач на тему «Повторение опытов»
Задача 1. Предприятие имеет проблемы с поставками сырья. Вероятность
того, что в каждом отдельном месяце предприятие будет полностью обеспечено
сырьем, равна 0,9. Какова вероятность того, что за полугодовой период
предприятие будет полностью обеспечено сырьем:
а) ровно в трех месяцах?
б) не менее чем в двух месяцах?
Решение.
а)Поскольку вероятность обеспечения
предприятия сырьем в каждом отдельном месяце постоянна и не зависит от
обеспеченности сырьем в других месяцах, то мы имеем схему Бернулли.
Следовательно, вероятности обеспечения сырьем могут быть рассчитаны по закону
Бернулли:
, где:
- вероятность обеспечения предприятия сырьем в m месяцах за n месяцев;
p - вероятность обеспечения предприятия сырьем в каждом месяце, р = 0,9;
q - вероятность не обеспечения предприятия сырьем в каждом
месяце, q = 1 – p
= 0,1.
n – количество месяцев в полугодии, n
= 6;
m – число месяцев обеспечения сырьем;
Cnm – число сочетаний
из n = 6 по m, 
;
а) n = 6; m = 3, получим:
б) Т.к. события «не менее чем в двух месяцах» и «менее чем в
двух месяцах» противоположные, то: 
;
;
получим: 
.
Ответ: а) Р(А) = 0,015; б) Р(А) = 0,999945.
Задача 2. Два ревизора проверяют счета фирмы. Каждый случайным образом
выбрал по 10 счетов. Известно, что вероятность наличия ошибочного счета среди
счетов фирмы равна 0,05. Какова вероятность того, что:
а) каждый ревизор обнаружит
хотя бы один ошибочный счет;
б) будет обнаружен
хотя бы один ошибочный счет?
Решение.
Исходим
из посылок:
- если среди
выбранных счетов есть ошибочный, то ревизор его обнаруживает;
- ревизоры
действуют независимо друг от друга (обнаружение ошибочного счета одним
ревизором не влияет на возможность обнаружения ошибочного счета другим
ревизором).
Обозначим:
А – событие,
состоящее в том, что каждый ревизор обнаружит хотя бы один ошибочный счет;
В
– событие, состоящее в том, что первый ревизор обнаружит хотя бы один ошибочный
счет;
– событие, состоящее в
том, что первый ревизор не обнаружит ни одного ошибочного счета;
С – событие,
состоящее в том, что второй ревизор обнаружит хотя бы один ошибочный счет;
– событие, состоящее в
том, что второй ревизор не обнаружит ни одного ошибочного счета.
p - вероятность наличия ошибочного счета среди счетов фирмы;
q - вероятность отсутствия ошибочного счета среди счетов фирмы.
D – событие, состоящее в том, что будет обнаружен хотя бы один
ошибочный счет;
а) Очевидно А = В∙С,
отсюда Р(А) = Р(В∙С) = Р(В)∙Р(С)
– т.к. ревизоры действуют независимо.
Но Р(В) = 1 – Р() и Р(С) = 1 - Р(
), тогда Р(А) = (1 –
Р())∙(1 - Р()).
По условию
вероятность наличия ошибочного счета среди счетов фирмы постоянна, равна 0,05 и
не зависит ни от количества выбранных счетов ни от номера ревизора,
следовательно, мы имеем дело со схемой Бернулли и поэтому:
Р()=Р()= 
Получаем:
Р(А)=(1–0,5987)∙(1-0,5987) = 0,1610.
б) Очевидно, что D
= B + C , отсюда:
Р(D) = Р(B + C) = P(B) +P(C) – P(B)∙P(C) – т.к. события B и C – совместные.
Но: Р(В) = 1 – Р(), Р(С) = 1 - Р(), P(B)∙P(C) = (1 – Р())∙(1 - Р()),
Получаем: Р(D)
= (1 – 0,5987) + (1 – 0,5987) - - (1 – 0,5987)∙(1 - 0,5987) = 0,642.
Ответ: а) Р(А) = 0,1610; б)
Р(D) = 0,6420.
Задача 3. Происходит демонстрация работы нового разрабатываемого фирмой
изделия потенциальному заказчику. Демонстрируется работа трех изделий. Для
каждого изделия вероятность того, что демонстрация пройдет без каких-либо
сбоев, равна 0,9. Если все три изделия отработают без сбоев, вероятность того,
что клиент сделает заказ, равна 0,8. Если одно из изделий допустит сбой,
вероятность заказа равна 0,6; если два изделия допустят сбой, вероятность
заказа уменьшается до 0,3. Если неполадки будут в работе всех трех изделий,
заказа точно не будет. Какова вероятность того, что клиент сделает заказ?
Решение.
Обозначим:
А – событие,
состоящее в том, что клиент сделает заказ;
В
– событие, состоящее в том, что все три изделия отработают без сбоев;
С
– событие, состоящее в том, что одно из изделий допустит сбой;
D – событие, состоящее в том, что два изделия допустят сбой;
Опишем событие А: А
= ВА + СА + DА, соответственно
Р(А) = Р(ВА + СА + DА)
= Р(ВА) + Р(СА) + Р(DА)= = Р(В)∙Р(А/В) + Р(С)∙Р(А/С)
+ Р(D)∙Р(A/D), т.к. события ВА, СА и DA – несовместные.
Поскольку
вероятность отсутствия сбоев в работе каждого изделия постоянна и не зависит от
сбоев в работе других изделий, то мы имеем схему Бернулли. Следовательно,
вероятности событий В, С, D могут быть
рассчитаны по закону Бернулли:
, где:
- вероятность появления сбоев в работе m
изделий в партии из n изделий;
p - вероятность работы каждого изделия без сбоев, р = 0,9;
q - вероятность сбоев в работе каждого изделия, q = 1 – p = 0,1.
n – количество изделий в партии, n
= 3;
m – число изделий, отработавших без сбоя в работе;
Cnm – число сочетаний
из n = 3 по m, ;
По условию:Р(А/В)=0,8; Р(А/С)=0,6; Р(А/D)= 0,3;
Получим:
Р(А) = 0,729∙0,8 + 0,243∙0,6 + +0,027∙0,3 = 0,7371.
Ответ:
Р(А) = 0,7371.
Задача 4. Владелец универсама считает, что в среднем каждый пятый посетитель
его магазина совершает покупку. Допуская, что предположение владельца верно,
определить вероятность того, что
а) двое из восьми
посетителей универсама совершают покупки;
б) хотя бы один из
пяти посетителей универсама совершит покупку.
Решение.
Поскольку
вероятность покупки для каждого посетителя постоянна и не зависит от совершения
покупок другими посетителями, то мы имеем схему Бернулли. Следовательно,
вероятности совершения покупок посетителями могут быть рассчитаны по закону
Бернулли:
, где:
- вероятность совершения покупок m
посетителями из совокупности в n посетителей;
p - вероятность совершения покупки каждым посетителем, р = 0,2;
q - вероятность не совершения покупки каждым посетителем, q = 1 – p = 0,8.
n – количество посетителей в совокупности;
m – количество посетителей совершивших покупки;
Cnm – число сочетаний
из n по m, ;
а) n = 8; m = 2, получим:
;
б) т.к. события
«хотя бы один из пяти» и «ни одного из пяти» противоположные, то:
;
получим: 
.
Ответ: а) Р(А) = 0,293; б) Р(А) = 0,6723.
Задача 5. Отдел контроля качества фирмы, производящей стереофонические
системы, взял на проверку 4 системы. Вероятность обнаружения дефекта в каждой
из них составляет 0,02. Какова вероятность, что
а) во всех системах
будут обнаружены дефекты;
б) хотя бы в одной
системе будут обнаружены дефекты?
Решение.
Поскольку
вероятность обнаружения дефекта в каждой системе постоянна и не зависит от
обнаружения дефекта в других системах, то мы имеем схему Бернулли.
Следовательно, вероятности обнаружения дефекта в системах могут быть рассчитаны
по закону Бернулли:
, где:
- вероятность обнаружения дефекта в m системах из
совокупности в n систем;
p - вероятность обнаружения дефекта в каждой системе, р = 0,02;
q - вероятность не обнаружения дефекта в каждой системе, q = 1 – p = 0,98.
n – количество систем в совокупности;
m – количество дефектных систем;
Cnm – число сочетаний
из n по m, ;
а) n = 4; m = 4, получим:
;
б) т.к. события
«хотя бы в одной из четырех» и «ни в одной из четырех» противоположные, то: 
;
;
получим: 
.
Ответ: а) Р(А) = 0,00000016; б) Р(А) = 0,0776.
Задача 6. В работе
телефонной станции происходят в среднем 3 сбоя в час. Определить вероятность:
а) пяти сбоев за 2
часа;
б) хотя бы одного
сбоя за 1 час.
Решение.
Поскольку
число соединений в работе телефонной станции в течении часа гораздо больше
числа сбоев в ее работе (числа неверных соединений), то вероятность появления m сбоев вычисляется по
закону Пуассона с параметром λ = 3 (сбоя в час): Рm = 
.
а) Обозначим:
А – событие,
состоящее в появлении пяти сбоев за 2 часа работы станции.
В соответствии со
свойством закона Пуассона вероятность пяти сбоев за 2 часа определится по этому
же закону, но при λ =2∙3=6 (сбоев в час):
Р(А)=Р5 =
- этот же результат
можно получить из таблицы распределения Пуассона при: λ = 6
и m
= 5.
б) Обозначим:
А – событие,
состоящее в появлении хотя бы одного сбоя за 1 час работы станции;
– событие, состоящее в
отсутствии сбоев за 1 час работы станции.
Тогда: Р(А)=1–Р()=1–Р0 =1-
.
Ответ: а) Р(А) = 0,1606; б)
Р(А) = 0,9502.
Задача 7. В агентство по продаже недвижимости в среднем обращаются 8
клиентов в день. Какова вероятность того, что за данный день в агентство
обратятся 3 клиента?
Решение.
В
задаче задана интенсивность потока событий λ = 8 клиентов в день.
Поскольку время обращения клиента в агентство гораздо менее времени работы
агентства и самих обращений – немного, то можно считать, что вероятность
обращения m клиентов в агентство вычисляется по закону Пуассона с параметром λ = 8
(обращений в день): Рm = . Тогда вероятность обращения трех клиентов в день
определится:
Р(А) = Р3 = 
- этот же результат
можно получить из таблицы распределения Пуассона при: λ = 8
и m
= 3.
Ответ:
Р(А) = 0,0286.
Задача 8. В честь национального праздника состоялся массовый забег на
дистанцию 10 км. В забеге приняли участие 250 человек. Обычно в забегах такого
типа из каждых десяти участников 8 доходят до финиша. Какова вероятность того,
что до финиша дойдут
а) 200 человек;
б) от 180 до 220
человек?
Решение.
Поскольку
считается, что вероятность дойти до финиша для каждого участника одинаковая, то
мы имеем схему Бернулли при большом числе испытаний. Следовательно,
вероятности, в данном случае, могут быть рассчитаны по:
а) локальной
теореме Муавра-Лапласа, представляющей собой первую предельную форму закона
Бернулли: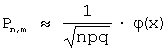 
, где:
- вероятность того, что из n
участников до финиша добегут m участников;
p - вероятность добежать до финиша для каждого участника, р = 0,8;
q - вероятность не добежать до финиша для каждого участника, q = 1 – p = 0,2.
n – количество участников, m
= 250;
- значение функции Гаусса в точке х, определяемое по таблицам;
х – значение
аргумента функции Гаусса, определяемое по формуле: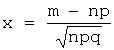 
;
б) интегральной
теореме Муавра-Лапласа, представляющей вторую предельную форму закона
Бернулли: 
, где:
- вероятность того, что из n
участников до финиша добегут от m1 до m2 участников;
- значение функции Лапласа в точке х, определяемое по таблицам;
х – значение
аргумента функции Лапласа, определяемое по формулам:
; 
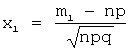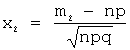
p - вероятность добежать до финиша для каждого участника, р = 0,8;
q - вероятность не добежать до финиша для каждого участника, q = 1 – p = 0,2.
n – количество участников, m
= 250;
Для а) имеем: n = 250; m = 200, р = 0,8;
q=0,2; получим: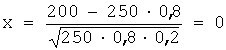 
; 
;отсюда:
;
Для б) имеем: n = 250; m1 = 180; m2 = 220; р = 0,8; q = 0,2; получим:
; 
т.к. функция Лапласа нечетная: Ф(-х)=-Ф(х),
то:
.
Ответ:а) 
; б) 
.
Задача 9. Что вероятнее выиграть у равносильного шахматиста (ничейный
исход партии исключается): больше одной партии из четырех или больше двух
партий из пяти.
Решение.
Поскольку партнеры
равносильны, то вероятность выигрыша равна вероятности проигрыша, причем эти
вероятности постоянны и не зависят от результатов предыдущих партий. Значит,
вероятности выигрыша могут быть рассчитаны по закону Бернулли:
, где:
- вероятность m выигрышей в n партиях;
p - вероятность выигрыша в каждой партии, р = 0,5;
q - вероятность проигрыша в каждой партии, q = p = 0,5;
n – количество сыгранных партий;
m – количество выигранных партий;
Cnm – число сочетаний
из n по m, ;
Событие «больше
одной партии из четырех» противоположно событию «не более одной партии из
четырех», которое в свою очередь равно сумме несовместных событий «ни одной из четырех»
и «одна из четырех», тогда: 
;
получим: 
; отсюда:
;
Событие «больше
двух партий из пяти» противоположно событию «не более двух партий из пяти»,
которое в свою очередь равно сумме несовместных событий «ни одной из пяти»,
«одна из пяти» и «две из пяти» тогда: 
;
получим:
;
; отсюда:
;
Следовательно: 
Ответ: У
равносильного шахматиста более вероятно выиграть более одной партии из четырех
чем более двух партий из пяти.
Задача 10. (Проблема Смита) В 1693 г. Джоном Смитом был поставлен следующий
вопрос: одинаковы ли шансы на успех у трех человек, если первому надо получить
хотя бы одну шестерку при бросании игральной кости 6 раз, второму не менее двух
шестерок при 12 бросаниях, а третьему - не менее трех шестерок при 18
бросаниях.
Решение.
Вероятности
получения различного числа шестерок при различном числе подбрасываний
игрального кубика могут быть рассчитаны по закону Бернулли:
, где:
- вероятность выпадения m
шестерок при n подбрасываниях;
p - вероятность выпадения шестерки при каждом подбрасывании, р = 
;
q - вероятность не выпадения шестерки при каждом подбрасывании, q =1 - p =
;
Cnm – число сочетаний
из n по m, ;
Событие «хотя бы одна шестерка при бросании
игральной кости 6 раз» противоположно событию «ни одной шестерки при бросании
игральной кости 6 раз», тогда:
получим:
;
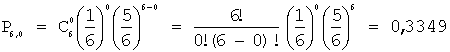Отсюда: 
;
Событие «не менее двух шестерок при 12
бросаниях» противоположно событию «менее двух шестерок при 12 бросаниях»,
которое в свою очередь равно сумме несовместных событий «ни одной шестерки при 12 бросаниях» и «одна шестерка
при 12 бросаниях», тогда:
получим:
;
;
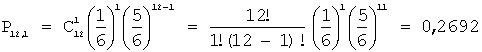Отсюда: 
;
Событие «не менее трех шестерок при 18
бросаниях» противоположно событию «менее трех шестерок при 18 бросаниях»,
которое в свою очередь равно сумме несовместных событий «ни одной шестерки при 18 бросаниях», «одна шестерка при 18 бросаниях» и «две
шестерки при 18 бросаниях», тогда:
;
получим:
;
;
;
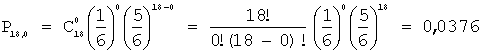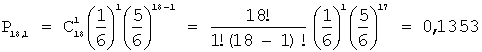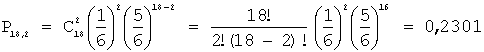Отсюда:
;
Следовательно: 
Ответ: Шансы на успех у трех человек
различны и снижаются с увеличением необходимого числа получения шестерок и
подбрасываний кубика.
