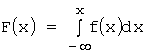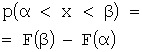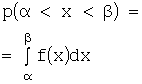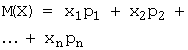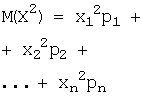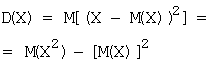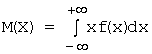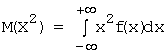СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

 

   Определение1.Случайная величина – переменная величина, которая случайным образом в результате опыта принимает некоторое числовое заранее неизвестное значение из определённого множества значений, при этом определена вероятность события, состоящего в том, что случайная величина примет это значение.

 

   Задание этой вероятности называется законом распределения случайной величины ( или ).

 

    Определение2.Случайной величиной X называется однозначная числовая функция , определенная на пространстве  элементарных  событий , которая каждому элементарному событию  ставит в соответствие число : . При этом должны быть определены вероятности элементарных событий.

   Для обозначения случайных величин обычно используются прописные буквы латинского алфавита X, Y, Z, … ;  соответствующие им строчные буквы x, y, z, … обозначают конкретные значения, которые они принимают.

   Различают два вида случайных величин – дискретные и непрерывные, в зависимости от типа множества значений.

 

   Дискретная случайная величина  принимает изолированные друг от друга числовые значения из конечного или бесконечного счетного множества значений, т.е. такого множества, элементы которого могут быть занумерованы и выписаны в последовательности ,, …, , …

 

   Непрерывная случайная величина принимает  неизвестные заранее значения из некоторого интервала:.

   Так число будущих генералов среди ста выпускников школы милиции – дискретная случайная величина с возможными значениями 0, 1, 2, …, 100, а дальность полета пули при выстреле – непрерывная и заранее неизвестная величина от 0 до 1 км.

 

Функция распределения случайной величины

 

   Случайные величины разнообразны по своей природе, происхождению, однако закон распределения можно записать в единообразной универсальной форме, а именно в виде функции распределения.

   Функцией распределения случайной величины Х называется функция F(х), выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х: .

   Геометрически, функция распределения интерпретируется как вероятность того, что случайная величина Х попадет левее заданной точки х числовой оси.

   Функцию F(х) называют также интегральной функцией распределения (или интегральным законом распределения).

 

   Свойства функции распределения:

 

1.Функция распределения случайной величины F(х) – неотрицательна, и ее значения заключены между нулем и единицей: .

2.Функция распределения F(х) есть неубывающая функция: .

3.Если непрерывная случайная величина Х определена на всей числовой оси, то

,   и    .

 

4.Если случайная величина Х принимает значения только на отрезке [a;b], то ее функция распределения F(x) такова: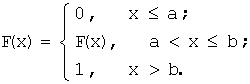

 

 

5.Вероятность попадания случайной величины Х в полуоткрытый интервал  равна приращению ее функции распределения на этом интервале:  

.

6.Функция распределения F(x) произвольной случайной величины Х непрерывна слева, то есть левый предел функции F(x) в точке а равен ее значению в точке а:

7.P(X≤a)=F(a+0), где правый предел функции в точке а;

 

или в более развернутом виде:

Р(Х≤a)=P(X<a)+P(X=a)=F(a)+P(X =a)=F(a+0);

Из этого равенства получаем: вероятность того, что случайная величина Х примет конкретное значение а, равная Р(Х=а):Р(Х=а)=F(а+0)–F(a).

 

Дискретные случайные величины

 

   Обычно закон распределения задаётся в виде таблицы, которая называется рядом распределения.

 

Здесь первая строка содержит всевозможные (конечные или бесконечные) значения случайной величины Х (обычно перечисляемые в порядке возрастания), то есть х₁, х₂, …, х_n…; а в другой строке указаны вероятности принятия случайной величины Х этих значений , то есть p₁=P(X=x₁), p₂=P(X=x₂), … , p_n=P(X=x_n) ….

Отметим, что события , , …,

 попарно несовместны и образуют полную группу, поэтому сумма их вероятностей равна единице: .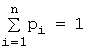

 

   Функция распределения дискретной случайной величины:

 для   ()

 

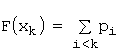 -есть разрывная ступенчатая кусочно-постоянная функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции F(х) равна 1.

 

   Пример. Дискретная случайная величина Х имеет ряд распределения:

Найти функцию распределения F(х).

Решение:Вычислим значения функции распределения 

.

 

В этой формуле суммируются лишь те вероятности p_k из ряда распределения, которые соответствуют значениям х_k, меньшим (расположенным левее) чем значение х, в котором вычисляется функция F(x).

   F(x)=0 для х≤-1 (так как x_k, меньших х в ряде распределения нет);

   F(x)=0,2 для -1<х≤0 (так как х₁=-1<х, и одно слагаемое р₁=0,2);

   F(x)=0,2+0,1=0,3 для 0<х≤2 (так как х₁=-1<x; x₂=0<x, и два слагаемых р₁=0,2; р₂=0,1);

   F(x)=0,2+0,1+0,3=0,6 для 2<х≤3 (так как

х₁=-1<x; x₂=0<x; х₃=2<x, и 3 слагаемых р₁=0,2; р₂=0,1; р₃=0,3);

   F(x)=0,2+0,1+0,3+0,2=0,8 для 3<х≤4 (так как х₁=-1<x; x₂=0<x; х₃=2<x; х₄=3<x и 4 слагаемых

р₁=0,2; р₂=0,1; р₃=0,3; p₄=0,2);

   F(x)=0,2+0,1+0,3+0,2+0,2=1 для 4<х (так как х₁=-1<x; x₂=0<x; х₃=2<x; х₄=3<x; x₅=4<x и 5 слагаемых р₁=0,2; р₂=0,1; р₃=0,3; p₄=0,2;p₅=0,2).

Таким образом: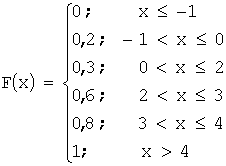

 

 

 

 

 

 

Непрерывные случайные величины

 

   Будем предполагать, что функция распределения непрерывной случайной величины непрерывна в любой точке области определения и дифференцируема всюду, кроме, может быть, конечного числа точек.

 

Плотность вероятности

 

   Плотностью вероятности  (плотностью распределения или просто плотностью) случайной величины Х называется производная от функции распределения: .

Плотность вероятности иногда также называют дифференциальным законом или дифференциальной функцией распределения.

 

   Свойства плотности вероятности:

1. Плотность вероятности – неотрицательная функция:  .

2.

 

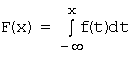
3.  Вероятность того, что непрерывная случайная величина Х примет значение х, принадлежащее

 

интервалу  () равна:

.

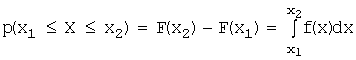4.Условие нормировки:.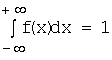

 

 

Сумма (разность, произведение) случайных величин X и Y

 

   Две случайные величины X и Y называются независимыми, если события  и  независимы для всех значений  и .

   Суммой (разностью, произведением) случайных величин X и Y называется случайная величина, обозначаемая как X+Y (X-Y, X·Y) которая принимает все возможные значения вида  (, ), где i=1,2,...,n  и j=1,2,…,m с вероятностями  того, что случайная величина X примет значение , а случайная величина Y примет значение :

.

В случае независимости X и Y :

.

 

Числовые характеристики случайных величин

 

Математическое ожидание

 

   Вероятностный смысл математического ожидания  заключается в том, что оно даёт среднее значение случайной величины.

   Математическое ожидание МX (или М(X)) дискретной случайной величины X определяется формулой: 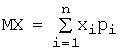. Непрерывной:  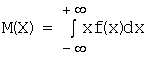(если интеграл сходится). 

 

   Свойства математического ожидания:

 

1.Если случайная величина x принимает одно и то же значение, то есть XºС, то её математическое ожидание равно С: М(С)=С.

2.Постоянный множитель можно выносить за знак математического ожидания: М(kX) = kMX, где k –константа.

3. Математическое ожидание алгебраической суммы двух (или более) случайных величин X и Y, определённых на одном и том же пространстве элементарных событий, равно алгебраической сумме их математических ожиданий: M(X+Y)=MX+MY.

4.Математическое ожидание произведения двух (или более) независимых случайных величин X и Y, определённых на одном и том же пространстве элементарных событий, равно произведению их математических ожиданий: М(XY) = МX×МY.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: М(X-МХ)=0. 

 

Дисперсия

 

   Дисперсия DX случайной величины X определяется формулой: DX = M(X – MX)²,

или, словами, дисперсия случайной величины - это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

   Для вычисления дисперсии используют формулу: .

   Для дискретной случайной величины формулу записывают так: DX = =.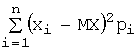

Для непрерывной: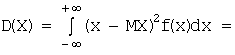 

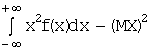 (если интеграл сходится).

 

   Дисперсия характеризует меру рассеяния (разбросанности) значений случайной величины относительно её математического ожидания. Если все значения случайной величины тесно сконцентрированы около её математического ожидания и большие отклонения от математического ожидания маловероятны, то такая случайная величина имеет малую дисперсию. Если значения случайной величины рассеяны и велика вероятность больших отклонений от математического ожидания, то такая случайная величина имеет большую дисперсию.

 

   Свойства дисперсии:

 

1.Дисперсия постоянной величины равна нулю: D(С)= 0.

2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(kX) = k² D(X).

3.Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:.

 

 

   Сведения о законах распределения вероятностей случайных величин представим для наглядности следующей таблицей: