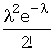Необходимо знать следующие распределения случайных величин:

а)биномиальное(Бернулли)  г)равномерное

б)Пуассона                д)показательное               

в)геометрическое          е)нормальное

                          (закон Гаусса)

Биномиальный закон распределения

 

   Определение.  Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами n и p[0,1], что символически обозначается как X ~ Bi(n, p), если вероятности того, что она примет значения 0,1,2,...,m,..., n, соответственно равны: ,где: q=1-p.

Отметим, что выражение  представляет собой формулу Бернулли.  Напомним, что формула Бернулли определяет вероятность того, что при проведении n испытаний (по схеме Бернулли), некоторое событие (вероятность появления которого равна p) произойдет ровно m раз.

Построим ряд распределения:

	0	1	2	…	m	…	n
				…		…

Проверим корректность записи закона распределения, для чего рассмотрим сумму всех вероятностей, стоящих во второй строке таблицы. Заметим, что эта строка содержит элементы разложения бинома Ньютона:

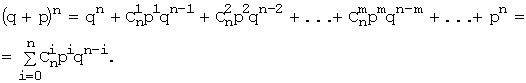
Поскольку , то:.

Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, соответственно равны: ,.

Закон распределения Пуассона

 

   Определение. Дискретная случайная величина Х имеет закон распределения Пуассона с параметром , что символически обозначается как , если вероятности того, что она примет значения 0,1,2,...,m,  соответственно равны:

.

Построим ряд распределения:

	0	1	2	…	m	…
				…		…

Проверим корректность записи закона распределения, для чего рассмотрим сумму всех вероятностей, стоящих во второй строке таблицы:

Заметим, что выражение  представляет собой разложение в ряд функции  при , т.е.: .

Поэтому: .

Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона, соответственно равны: M(X) = λ, D(X) = λ. Это характерная особенность распределения Пуассона.

 

 

Геометрическое распределение

 

   Определение.  Дискретная случайная величина Х имеет геометрическое распределение, если вероятность того, что она примет значение 1,2,3,...(счетное множество значений) соответственно равна: ,

где: p(0,1);  q=1-p.

Построим ряд распределения:

	1	2	3	…	m	…
				…		…

Проверим корректность записи закона распределения, для чего рассмотрим сумму всех вероятностей, стоящих во второй строке таблицы:

Заметим, что выражение  представляет собой сумму членов геометрической прогрессии (откуда и происходит название геометрического распределения) с первым членом, равным единице и знаменателем q. Используя известную формулу суммы бесконечного числа членов геометрической прогрессии, получим:.

Откуда:.

Математическое ожидание и дисперсия случайной величины Х, распределенной по геометрическому закону, соответственно равны:,  .

Геометрическое распределение тесно связано со схемой испытаний Бернулли, а, следовательно, с биномиальным распределением. Отличие состоит в том, что биномиальная случайная величина определяет вероятность m успехов в n испытаниях, а геометрическая - вероятность m  испытаний до первого успеха (включая первый успех).

Равномерный закон распределения

 

   Определение. Распределение вероятностей непрерывной случайной величины Х на интервале [a, b] называется равномерным, если плотность вероятности  f(х) постоянна на этом интервале и равна нулю вне него ,т.е.:

f(х) = C = const, если хÎ[a, b],

f(х) = 0, если хÏ[a, b].

Плотность вероятности обладает следующим свойством: . Подставляя, получим:

Откуда:  

.

Функция распределения F(X) может быть найдена путем интегрирования плотности вероятности: .

Таким образом: .

 

 

Математическое ожидание: ,

дисперсия: .

 

Показательный закон распределения

 

   Определение. Показательный(экспоненциальный) закон распределения непрерывной случайной величины Х задается плотностью вероятности:

.

Функция распределения:  

Математическое ожидание: ;

дисперсия:  ;

среднее квадратическое отклонение: .

Характерная особенность этого распределения – равенство математического ожидания среднему квадратическому отклонению.

 

 

Нормальный закон распределения(закон Гаусса)

 

   Определение. Нормальный закон распределения (закон Гаусса) непрерывной случайной величины Х задается плотностью вероятности :

,где:

а и s - параметры распределения, которые равны, соответственно, ее математическому ожиданию и среднему квадратическому отклонению, т.е. М(Х)= = а, дисперсия .

График плотности нормального распределения   представляет собой кривую симметричную относительно прямой x=a с ординатой, максимальной в точке x=a, и равной . Этот график называется кривой Гаусса.  

Функция распределения имеет вид:

Вероятность попадания случайной величины в интервал   записывается в виде: , где Ф(x)-функция Лапласа.

 

Функция Лапласа

   Функцией Лапласа Ф(x) называется интеграл как функция верхнего предела интегрирования:

.

Свойства функции Лапласа:

1) Ф(x) нечетная функция: Ф(-x)= -Ф(x)

2) Ф(-)= -0,5; Ф(+)= 0,5; Ф(0)=0.

Значения функции Лапласа Ф(x) приводятся в таблицах (приложение в конце пособия). При пользовании таблицами необходимо иметь ввиду, что при  Ф(x)0,5, при  Ф(x)-0,5 (с точностью до 0,0001).

   Рассмотрим два распределения, с которыми мы встретимся в дальнейшем, при изучении математической статистики.

 

 

 

Распределение Пирсона χ² (хи-квадрат)

 

   Карл Пирсон (Pearson, 1857-1936) английский математик и биолог. С целью проверки теории Дарвина разработал статистический метод, получивший широкое распространение при исчислении коэффициента корреляции между различными переменными. В частности, в 1900 г. им предложен критерий ‘хи-квадрат’. В литературе часто упоминается осуществленный Пирсоном опыт по экспериментальной проверке вероятности выпадания  герба при подбрасывании монеты. Из 24000 подбрасываний, герб выпал 12012 раз.

   Определение. Распределением χ² (хи квадрат) с n степенями свободы называется распределение суммы квадратов n независимых случайных величин, каждая из которых распределена по нормальному закону с параметрами MX= и DX=, т.е: ,

где: Z_i (i =1,2, …,n) - набор n независимых, нормально распределенных случайных величин.

   Плотность вероятности распределения χ² определяется  выражением:

  ,

где:  - гамма-функция Эйлера (можно показать, что для целых положительных значений аргумента гамма-функция Эйлера принимает более простой вид:  ).

  

Распределение Стьюдента

 

   Уильям Госсет (1876-1937) – английский статистик, писавший под псевдонимиом “Student” (стьюдент).

   Определение. Распределением Стьюдента (или -распределением) называется распределение случайной величины ,

где: Z - случайная величина, распределенная по нормальному закону с параметрами MX= и DX=, χ² – независимая от Z случайная величина, имеющая  распределение χ² с  n степенями свободы.