Примеры решения задач на тему «Случайные величины».

  

   Задача 1. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.

Решение. Возможные значения величины X: x₁ = 0; x₂ = 10 и x₃ = 50. Так как «пустых» билетов – 89, то p₁ = 0,89, вероятность выигрыша 10 у.е. (10 билетов) – p₂ = 0,10 и для выигрыша 50 у.е. – p₃ = 0,01. Таким образом:

X	0	10	50
P	0,89	0,10	0,01

Легко проконтролировать:.

 

   Задача 2. Вероятность того, что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее. Составить ряд распределения количества опрошенных покупателей.

Решение.  Согласно условию задачи р = 0,6. Откуда: q=1-p = 0,4. Подставив данные значения, получим:  и построим ряд распределения:

 

Х	1	2	…	m	…
pi	0,6	0,24	…		…

 

   Задача 3. Компьютер состоит из трех независимо работающих элементов: системного блока, монитора и клавиатуры. При однократном резком повышении напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения Бернулли составить закон распределения числа отказавших элементов при скачке напряжения в сети.

Решение. Рассмотрим распределение Бернулли (или биномиальное): вероятность того, что в n  испытаниях событие А появится ровно k раз: , или:

X	0	1	…	k	…	n
P	qn		…		…	pn

Вернёмся к задаче.

Возможные значения величины X (число отказов):

x₀ =0 – ни один из элементов не отказал;

x₁ =1 – отказ одного элемента;

x₂ =2 – отказ двух элементов;

x₃ =3 – отказ всех элементов.

Так как, по условию, p = 0,1, то q = 1 – p = 0,9. Используя формулу Бернулли, получим

, ,

, .

Контроль: .

Следовательно, искомый закон распределения:

 

X	0	1	2	3
p	0,729	0,243	0,027	0,001

 

   Задача 4. Произведено 5000 патронов. Вероятность того, что один патрон бракованный . Какова вероятность того, что во всей партии будет ровно 3 бракованных патрона?

Решение. Применим распределение Пуассона: это распределение используется для определения вероятности того, что при очень большом

 

количестве испытаний (массовые испытания), в каждом из которых вероятность события A очень мала, событие A наступит  k раз: 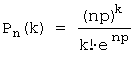, где .

Здесь n = 5000, p = 0,0002, k = 3. Находим  , тогда искомая вероятность: .

 

   Задача 5. При стрельбе до первого попадания с вероятностью попадания p = 0,6 при выстреле надо найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. Применим геометрическое распределение: пусть производятся независимые испытания, в каждом из которых событие A имеет вероятность появления p (и непоявления q = 1 – p). Испытания заканчиваются, как только произойдет событие A.

При таких условиях вероятность того, что событие A произойдет на k-ом испытании, определяется по формуле: . Здесь p = 0,6; q = 1 – 0,6 = 0,4;  k = 3. Следовательно, .

 

   Задача 6. Пусть задан закон распределения случайной величины X:

X	1	2
P	0,2	0,8

Найти математическое ожидание.

Решение. .

Заметим, что вероятностный смысл математического ожидания – это среднее значение случайной величины.

 

   Задача 7. Найти дисперсию случайной величины X со следующим законом распределения:

X	2	3	5
P	0,1	0,6	0,3

Решение. Здесь .

Закон распределения квадрата величины X²:

X2	4	9	25
P	0,1	0,6	0,3

.

Искомая дисперсия: .

Дисперсия характеризует меру отклонения (рассеяния) случайной величины от её математического ожидания.

 

   Задача 8. Пусть случайная величина задается распределением:

X	2м	3м	10м
P	0,1	0,4	0,5

Найти её числовые характеристики.   

Решение: м, м²,

м²,   м.

Про случайную величину X можно сказать либо – ее математическое ожидание 6,4 м с дисперсией 13,04 м², либо – ее математическое ожидание 6,4 м с отклонением  м. Вторая формулировка, очевидно, нагляднее.

   Задача 9. Случайная величина X задана функцией распределения: .

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале .

Решение. Вероятность того, что X примет значение из заданного интервала, равно приращению интегральной функции в этом интервале, т.е. . В нашем случае  и , поэтому

.

 

   Задача 10. Дискретная случайная величина X задана законом распределения:

Найти функцию распределения F(x) и построить ее график.

Решение. Так как функция распределения,

 для , то

при  ;

при  ;

при  ;

при  ;

Соответствующий график:

 

   Задача 11. Непрерывная случайная величина X задана дифференциальной функцией распределения: .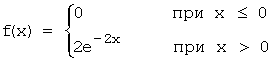

Найти вероятность попадания X в интервал

.

Решение. Заметим, что это частный случай показательного закона распределения.

Воспользуемся формулой: .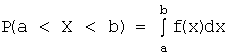

.

 

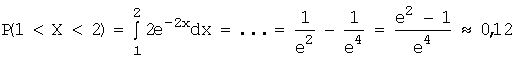   Задача 12. Найти числовые характеристики дискретной случайной величины X, заданной законом распределения:

X	–5	2	3	4
p	0,4	0,3	0,1	0,2

Решение. Математическое ожидание:

.

Запишем закон распределения X²:

X2	25	4	9	16
p	0,4	0,3	0,1	0,2

Математическое ожидание:

.

Находим дисперсию:

, .

 

   Задача 13. Непрерывная случайная величина задана на интервале  плотностью распределения , а вне этого интервала . Найти ее числовые характеристики.

Решение. Математическое ожидание:

.

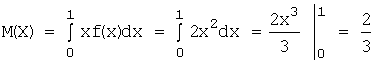Дисперсия: .

Среднее квадратическое отклонение: .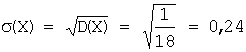

   

   Задача 14. Найти числовые характеристики случайной величины X, равномерно распределенной на интервале .

Решение. Для случайной величины, равномерно распределеной на интервале , плотность распределения: ,

поэтому: ; ;   .  

 

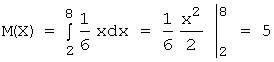   Задача 15. Математическое ожидание нормально распределенной случайной величины  , а среднее квадратическое отклонение - . Найти вероятность того, что в результате испытания X примет значение из интервала  и записать закон распределения.

Решение. Запишем вначале закон распределения. Общая формула имеет вид: .

Подставляя  и , получим: .

Вероятность того, что X примет значение из интервала  имеет вид:

, где 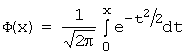– функция Лапласа.

Значения этой функции находятся с помощью таблицы.

В нашем случае: .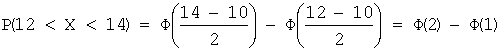

По таблице находим: , следовательно:

.